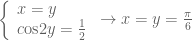Tháng Chín | 2011 | Nguyễn Anh Tuấn - Giáo viên Toán Trường THPT Lê Quảng Chí

Lưu trữ

Archive for Tháng Chín, 2011

Phương trình thuần nhất bậc hai, bậc ba đối với sinX và cosX

09/24/2011 tuanhien2011 2 bình luận

I- KIẾN THỨC CẦN NHỚ

NHÓM I: Phương trình thuần nhất bậc hai, bậc ba đối với một hàm số lượng giác

Dạng 1:

${\rm{a}}{\sin ^2}X + b\sin X\cos X + c{\cos ^2}X = d\left( 1 \right)\left( {a,b,c,d \in R} \right)$

Cách giải 1:

Xét $X = \frac{\pi }{2} + k\pi \left( {k \in Z} \right)$ $\Leftrightarrow \left\{ \begin{array}{l} {\sin ^2}X = 1 \\ \cos X = 0 \\ \end{array} \right.$

Thay vào phương trình (1) để kiểm tra.

Khi $X \ne \frac{\pi }{2} + k\pi \left( {k \in Z} \right)$ . Chia hai vế của phương trình (1) cho ${\cos ^2}X$ ta được phương trình:

$\left( {a - d} \right){\tan ^2}X + b\tan X + c - d = 0$

Cách giải 2: Phương trình (1) tương đương với phương trình sau:

$a\frac{{1 - c{\rm{os}}2X}}{2} + \frac{b}{2}\sin 2X + c\frac{{1 + c{\rm{os}}2X}}{2} = d$ $\Leftrightarrow b\sin 2X+ \left( {c-a} \right)c{\rm{os}}2X=2d-a-c$

Dạng 2:

${\rm{a}}{\sin ^3}X + b{\sin ^2}X\cos X + c\sin X{\cos ^2}X + d{\cos ^3}X = 0\left( 2 \right)$

Cách giải: Dạng toán này được giải theo như cách một ở trên

NHÓM II

II- MỘT SỐ VÍ DỤ

NHÓM I

Ví dụ 1: Giải phương trình sau

${\sin ^2}x + 3\sin x\cos x - 4{\cos ^2}x=0\left(* \right)$

Giải:

Cách 1:

Xét $x = \frac{\pi }{2} + k\pi \left( {k \in Z} \right)$

Khi đó, phương trình $\left(* \right)$ tương đương với phương trình ${\sin ^2}x = 0$

Vậy $x = \frac{\pi }{2} + k\pi \left( {k \in Z} \right)$ không phải là nghiệm của phương trình $\left(* \right)$

Chia hai vế của phương trình $\left(* \right)$ cho ${\cos ^2}x$ ta được phương trình sau:

${\tan ^2}x + 3\tan x - 4 = 0$

$\Leftrightarrow \tan x=1 \vee \tan x =-4$

$\Leftrightarrow x =\frac{\pi}{4}+k\pi \vee x = \arctan \left({- 4}\right)+k\pi$ $k \in Z$

Đáp số: $\boxed{x =\frac{\pi}{4}+k\pi ;x = \arctan \left({- 4}\right)+k\pi }$ $k \in Z$

Cách 2:

Phương trình đã cho tương đương với phương trình sau

$\frac{{1 - c{\rm{os}}2x}}{2} + \frac{3}{2}\sin 2x - 4\frac{{1 + c{\rm{os}}2x}}{2} = 0$

$\Leftrightarrow 3\sin 2x - 3\cos 2x = 1$

$\Leftrightarrow \sin \left( {2x - \frac{\pi }{4}} \right) = \frac{1}{{3\sqrt 2 }}$

Phương trình trên là phương trình bậc nhất đối với sinX và cosX

Ví dụ 2: Giải phương trình

$2{\sin ^2}x + 3\sqrt 3 \sin x.\cos x - c{\rm{o}}{{\rm{s}}^2}x = 2$

Ví dụ 3: Giải phương trình

$2co{{\mathop{\rm s}\nolimits} ^3}x + 2\sin x.{\cos ^2}x - {\rm{si}}{{\rm{n}}^3}x = 0$

NHÓM II

Ví dụ 4: Giải phương trình

$co{{\mathop{\rm s}\nolimits} ^3}x + \sin x - 3{\rm{si}}{{\rm{n}}^2}x\cos x = 0$

Ví dụ 5: Giải phương trình

$\tan x{\sin ^2}x - 2{\rm{si}}{{\rm{n}}^2}x = 3\left( {\cos 2x + \sin x\cos x} \right)$

BÀI TẬP

Giải các phương trình sau:

1. ${\sin ^3}\left( {x - \frac{\pi }{4}} \right) = \sqrt 2 \sin x$

2. ${\rm{si}}{{\rm{n}}^2}x + 2c{\rm{o}}{{\rm{s}}^2}x = 3\sin x\cos x$

3. $2{\sin ^2}x + 3{\cos ^2}x - c{\rm{os}}2x - 5\sin 2x = 0$

4. ${\rm{si}}{{\rm{n}}^2}x\left( {\tan x + 1} \right) = 3\sin x\left( {\cos x - \sin x} \right) + 3$

5. $4{\sin ^3}x + 3{\cos ^3}x - 3\sin x - {\sin ^2}x\cos x = 0$

6. $c{\rm{o}}{{\rm{s}}^3}x + {\sin ^3}x = \sin x - \cos x$

7. $\sin 3x + c{\rm{os}}3x = - 2\cos x$

8. $\sin x.\sin 2x + \sin 3x = 6{\cos ^3}x$

9. $2{\cos ^3}x = \sin 3x$

Chuyên mục:Các bài viết

Đề ra kì 1

09/12/2011 tuanhien2011 3 bình luận

Bài 1: Giải phương trình sau:

$\sqrt {{x^3}-1} ={x^2}+3x-1$

Bài 2: Giải phương trình sau :

$\sqrt {7{x^2}+25x+19} -\sqrt {{x^2}-2x-35} =7\sqrt {x+2}$

Bài 3: Giải hệ phương trình :

$\left\{ \begin{array}{l} \sqrt {x + y} + \sqrt {x - y} = 4 \\ {x^2} + {y^2} = 128 \\ \end{array} \right.$

Bài 4: Cho $a,b,c > 0$ . Chứng minh rằng:

$\frac{{{a^3}b}}{{1 + a{b^2}}} + \frac{{{b^3}c}}{{1 + b{c^2}}} + \frac{{{c^3}a}}{{1 + c{a^2}}} \ge \frac{{abc\left( {a + b + c} \right)}}{{1 + abc}}$

Bài 5: Cho $x,y,z > 0$ và $x + y + z = 7$ . Tìm giá trị lớn nhất của biểu thức :

$P = 15x + 8xy + 4xyz$

( ĐANG POST ĐÁP ÁN )

Chuyên mục:Đề thi Toán

Những bài toán hay về lượng giác

09/05/2011 tuanhien2011 2 bình luận

Cho $0 < x;y < \frac{\pi }{2}$ và $\frac{\pi }{3} \le x+y<\frac{\pi }{2}$

Giải phương trình sau: $\cos(x+y)\sin x\sin y=\frac{1}{8}$

Lời giải 1: ( Theo maxmin )

Do 
Vậy:

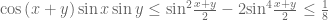
Lời giải 2: ( Theo longtoanlqc )

Không giảm tính tổng quát giả sử:(*)
Xét hàm số: 
,vì (*) và giải thiết ta suy ra được :

Suy ra 
Do đó  nghịch biến, ta được:

Vì vậy từ pt ta suy ra